Fundamentally fastest optical processes at the surface of a topological insulator

摘要

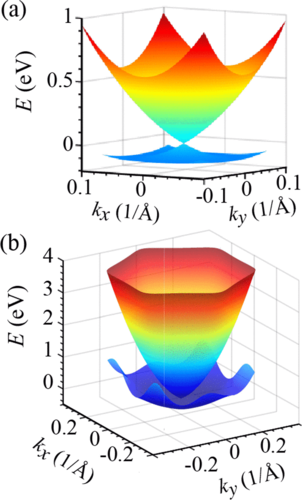
We predict that a single oscillation of a strong optical pulse can significantly populate the surface conduction band of a three-dimensional topological insulator, Bi$_2$Se$_3$. Both linearly- and circularly-polarized pulses generate chiral textures of interference fringes of population in the surface Brillouin zones. These fringes constitute a self-referenced electron hologram carrying information on the topology of the surface Bloch bands, in particular, on the effect of the warping term of the low-energy Hamiltonian. These electron-interference phenomena are in sharp contrast to graphene where there are no chiral textures for a linearly-polarized pulse and no interference fringes for circularly-polarized pulse. These predicted reciprocal space electron-population textures can be measured experimentally by time resolved angle resolved photoelectron spectroscopy (TR-ARPES) to gain direct access to non-Abelian Berry curvature at topological insulator surfaces.