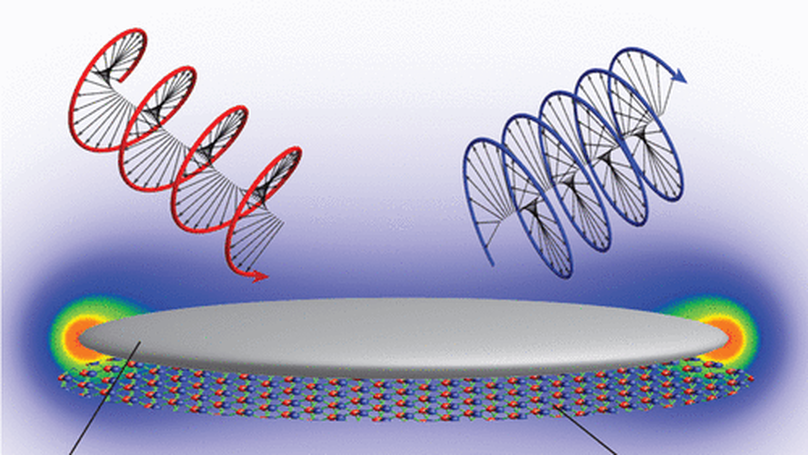
We theoretically study a topological nanospaser, which consists of a silver nanospheroid and MoS$_2$ monolayer flake of a circular shape. The metal nanospheroid acts as a plasmonic nanoresonator that supports two rotating modes, which are coupled to the corresponding valleys of MoS2. We apply external circularly polarized light that selectively pumps only one of the valleys of MoS$_2$. The generated spaser dynamics strongly depends on the size (radius) of the MoS$_2$ nanoflake. For a small radius, the system has only one spasing regime when only the chirally matched plasmon mode is generated, while at a larger size of MoS$_2$, depending on the pump intensity, there are two regimes. In one regime, only the chirally matched plasmon mode is generated, while in the other regime both chirally matched and chirally mismatched modes exist. Different regimes of spaser operation also have opposite handedness of the far-field radiated spaser system. Such a topological nanospaser has potential applications in different areas of infrared spectroscopy, sensing, probing, and biomedical treatment.

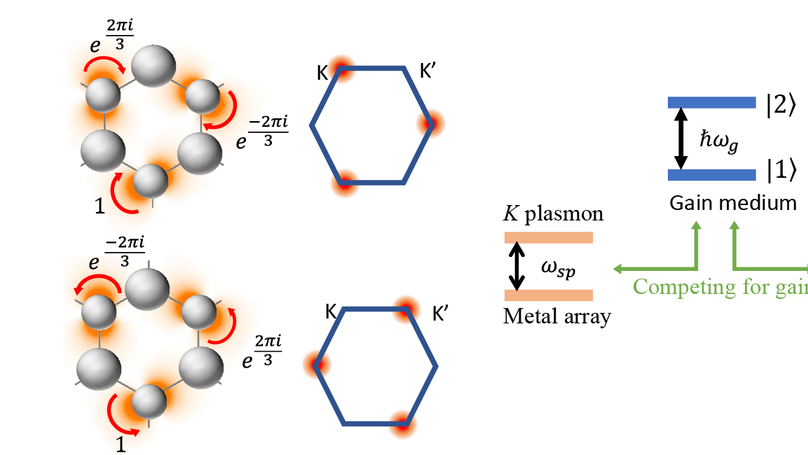
We theoretically introduce a topological spaser, which consists of a hexagonal array of plasmonic metal nanoshells containing an achiral gain medium in their cores. Such a spaser can generate two mutually time-reversed chiral surface plasmon modes in the valleys $K$ and $K'$, which carry the opposite topological charges $\pm 1$, and are described by a two-dimensional $E'$ representation of the $D_{3h}$ point symmetry group. Due to the mode competition, this spaser exhibits a bistability$:$ only one of these two modes generates, which is a spontaneous symmetry breaking. Such a spaser can be used for an ultrafast all-optical memory and information processing, and biomedical detection and sensing with chirality resolution.

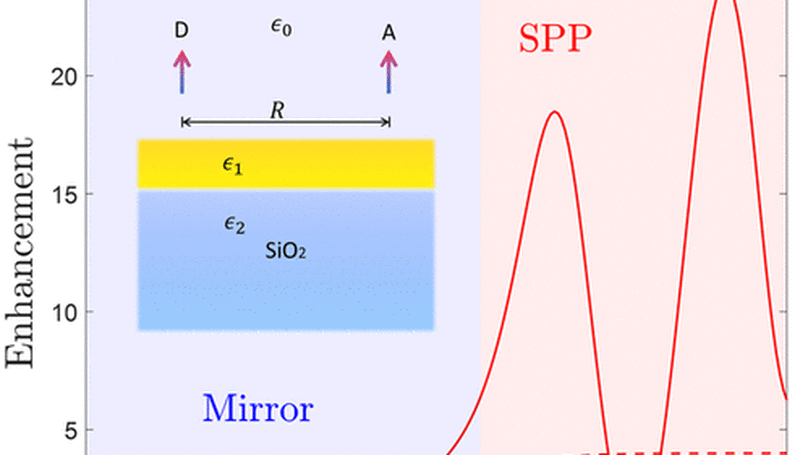
We investigate resonance energy transfer (RET) between a donor–acceptor pair above a gold surface (including bulk and thin-film systems) and explore the distance/frequency dependence of RET enhancements using the theory we developed previously. The mechanism of RET above a gold surface can be attributed to the effects of mirror dipoles, surface plasmon polaritons (SPPs), and retardation. To clarify these effects on RET, we analyze the enhancements of RET by the mirror method, the decomposition of s- and p-polarization, and the SPP dispersion of charge-symmetric and charge-antisymmetric modes. We find a characteristic distance (approximately 1/10 of the wavelength) that can be used to classify the dominant effect on RET. Moreover, the characteristic distance can be shortened by narrowing the thickness of the thin-film systems, indicating that SPPs can enhance the rate of RET at a short range. The charge-symmetric and charge-antisymmetric modes of the thin films also allow us to engineer the maximum RET enhancement. We hope that our analysis inspires further investigation into the mechanism of RET coupled with SPPs and its applications.

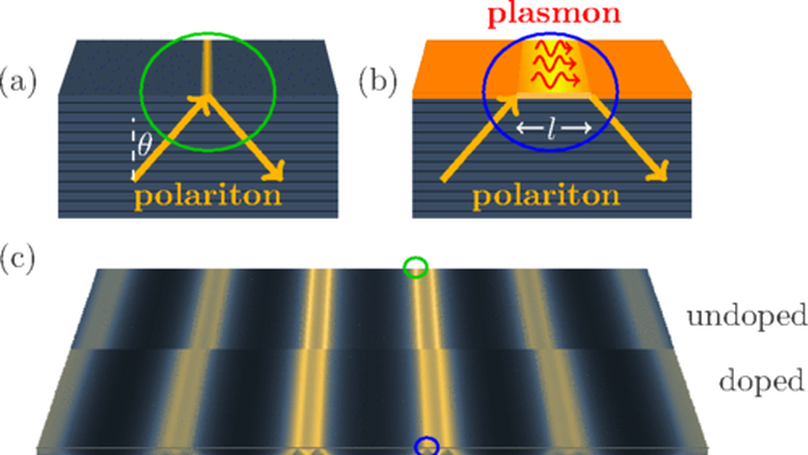
We present a theoretical analysis showing that layered topological insulators, for example, Bi$_2$Se$_3$ are optically hyperbolic materials in the range of terahertz (THz) frequencies. As such, these topological insulators possess deeply subdiffractional, highly directional collective modes$:$ hyperbolic phonon polaritons. We predict that in thin crystals the dispersion of these modes is split into discrete subbands and is strongly influenced by electron surface states. If the surface states are doped, then hybrid collective modes result from coupling of the phonon polaritons with surface plasmons. The strength of the hybridization can be controlled by an external gate that varies the chemical potential of the surface states. We also show that the momentum dependence of the plasmon-phonon coupling leads to a polaritonic analog of the Goos-Hänchen effect. The directionality of the polaritonic rays and their tunable Goos-Hänchen shift is observable via THz nanoimaging.

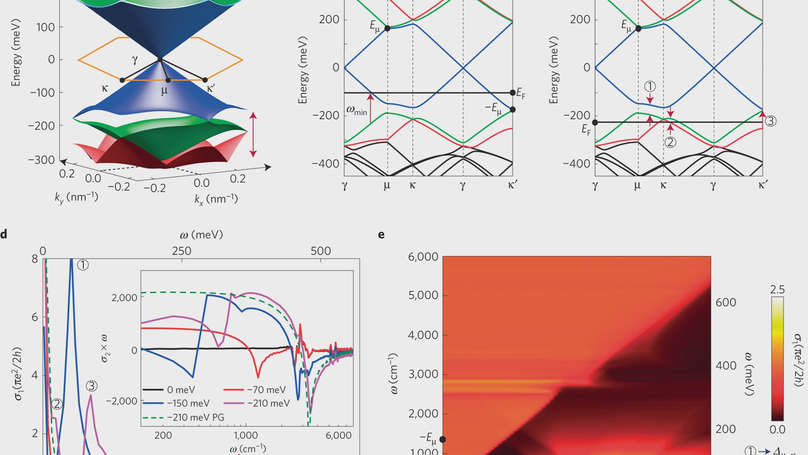
Moiré patterns are periodic superlattice structures that appear when two crystals with a minor lattice mismatch are superimposed. A prominent recent example is that of monolayer graphene placed on a crystal of hexagonal boron nitride. As a result of the moiré pattern superlattice created by this stacking, the electronic band structure of graphene is radically altered, acquiring satellite sub-Dirac cones at the superlattice zone boundaries. To probe the dynamical response of the moiré graphene, we use infrared (IR) nano-imaging to explore propagation of surface plasmons, collective oscillations of electrons coupled to IR light. We show that interband transitions associated with the superlattice mini-bands in concert with free electrons in the Dirac bands produce two additive contributions to composite IR plasmons in graphene moiré superstructures. This novel form of collective modes is likely to be generic to other forms of moiré-forming superlattices, including van der Waals heterostructures.

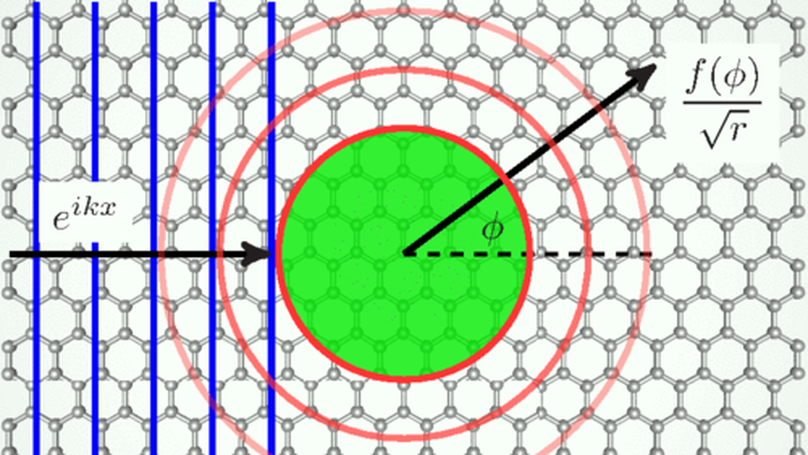
We calculate the differential, total, and transport cross-sections for scattering of two-dimensional massless Dirac electrons by a circular barrier. For scatterer of a small radius, the cross-sections are dominated by quantum effects such as resonant scattering that can be computed using the partial-wave series. Scattering by larger size barriers is better described within the classical picture of reflection and refraction of rays, which leads to phenomena of caustics, rainbow, and critical scattering. Refraction can be negative if the potential of the scatterer is repulsive, so that a $p$-$n$ junction forms at its boundary. Qualitative differences of this case from the $n$-$N$ doping case are examined. Quantum interference effects beyond the classical ray picture are also considered, such as normal and anomalous diffraction, and also whispering-gallery resonances. Implications of these results for transport and scanned-probe experiments in graphene and topological insulators are discussed.