Scattering of two-dimensional massless Dirac electrons by a circular potential barrier

摘要

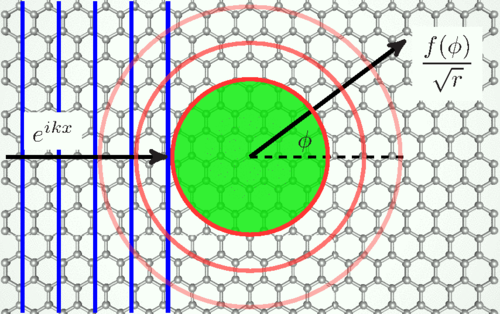
We calculate the differential, total, and transport cross-sections for scattering of two-dimensional massless Dirac electrons by a circular barrier. For scatterer of a small radius, the cross-sections are dominated by quantum effects such as resonant scattering that can be computed using the partial-wave series. Scattering by larger size barriers is better described within the classical picture of reflection and refraction of rays, which leads to phenomena of caustics, rainbow, and critical scattering. Refraction can be negative if the potential of the scatterer is repulsive, so that a $p$-$n$ junction forms at its boundary. Qualitative differences of this case from the $n$-$N$ doping case are examined. Quantum interference effects beyond the classical ray picture are also considered, such as normal and anomalous diffraction, and also whispering-gallery resonances. Implications of these results for transport and scanned-probe experiments in graphene and topological insulators are discussed.